算法复习笔记：贪心求最优 Caching 策略

题目来自 Algorithm design / Jon Kleinberg, Eva Tardos.—1st ed. 的 4.3 节。

参考文章：http://notebook.xyli.me/CS161/Intro-to-greedy-algo1/

问题背景

假设现在有一个容量为 $k$ 的缓存（cache）空间，和 $m$ 个内存 block 访问请求 $d_1, d_2, \dots, d_m$。对于第 $i$ 个请求 $d_i$，如果请求的 block 在缓存中，称其为一次命中（hit），否则称其为一次失效/缺页（miss）。若出现 miss，则需要从内存中读取该 block 并写入缓存（若缓存已满则会替换掉其中一个 block）。现给定请求序列，求一个最优缓存（caching）策略使得 miss 尽可能少。

Farthest-in-Future（FF）算法

算法内容

该算法的核心是，当 $d_i$ 需要被读取进内存时，将未来（首次）最晚出现（farthest in the future）的 block 替换掉。

例如：缓存内容为 $\{a, b, c, d, e, f\}$，请求队列为 $g, a, b, c, e, d, a, c, d, e, f, a, \dots$，当请求 $g$ 发生缺页时，缓存中 $f$ 在队列中首次最晚出现，因此将 $f$ 替换成 $g$。

下面证明该算法的正确性。

简化调度

首先引入一个新概念：简化调度（Reduced schedule）。简化调度的内容是，仅当某 block 被请求时才将其写入缓存。

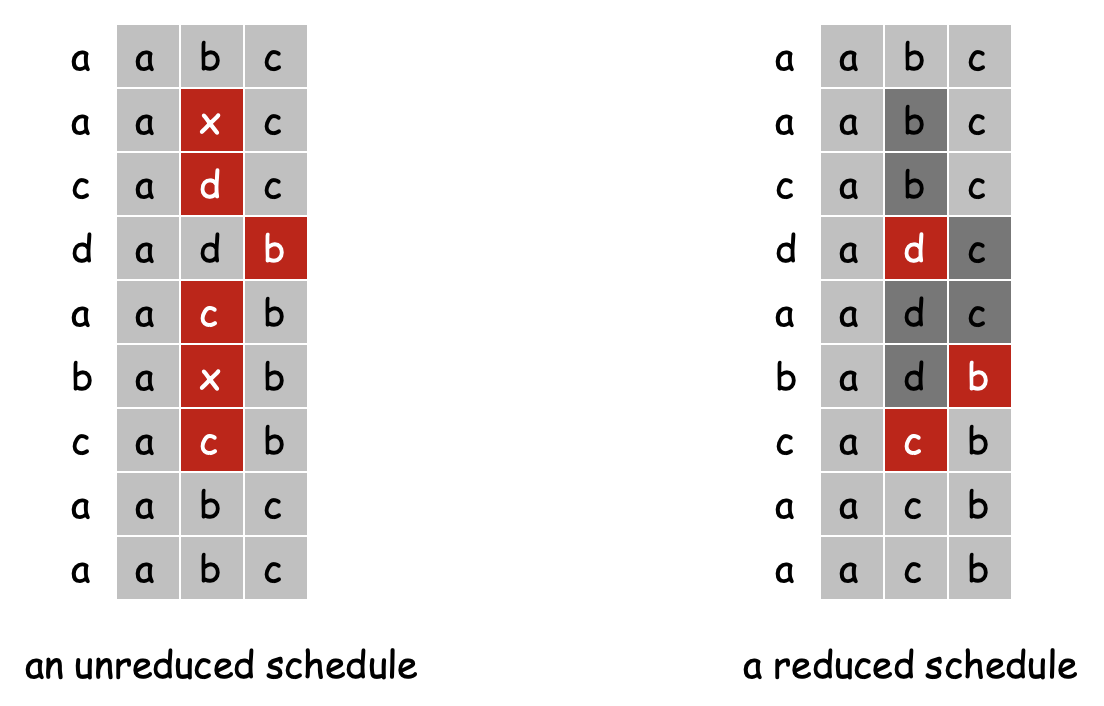
任何非简化调度（Non-reduced schedule）$S$ 可以在不增加 miss 次数*的情况下转化成简化调度 $S’$。

*：在非简化调度中，请求失败之外的 block 写入也被视为一次 miss（即换页，需要耗费大量时间从内存中读取数据）。

考虑某非简化调度 $S$，假设 $S$ 在 $t$ 时刻向内存中写入 $d$，但没有发生对 $d$ 的请求，则对于某时刻 $t’ > t$，有以下两种情况：

1. 写入 $d$ 后没收到对 $d$ 的请求，而是在 $t'$ 时刻收到了对另外一个不在内存中的 block（记作 $e$）的请求。此时省去 $d$ 的写入，可减少 1 次 miss。
2. 写入 $d$ 后在 $t'$ 时刻收到了对 $d$ 的请求。此时将写入 $d$ 的操作移至 $t'$ 时刻，miss 数不变。

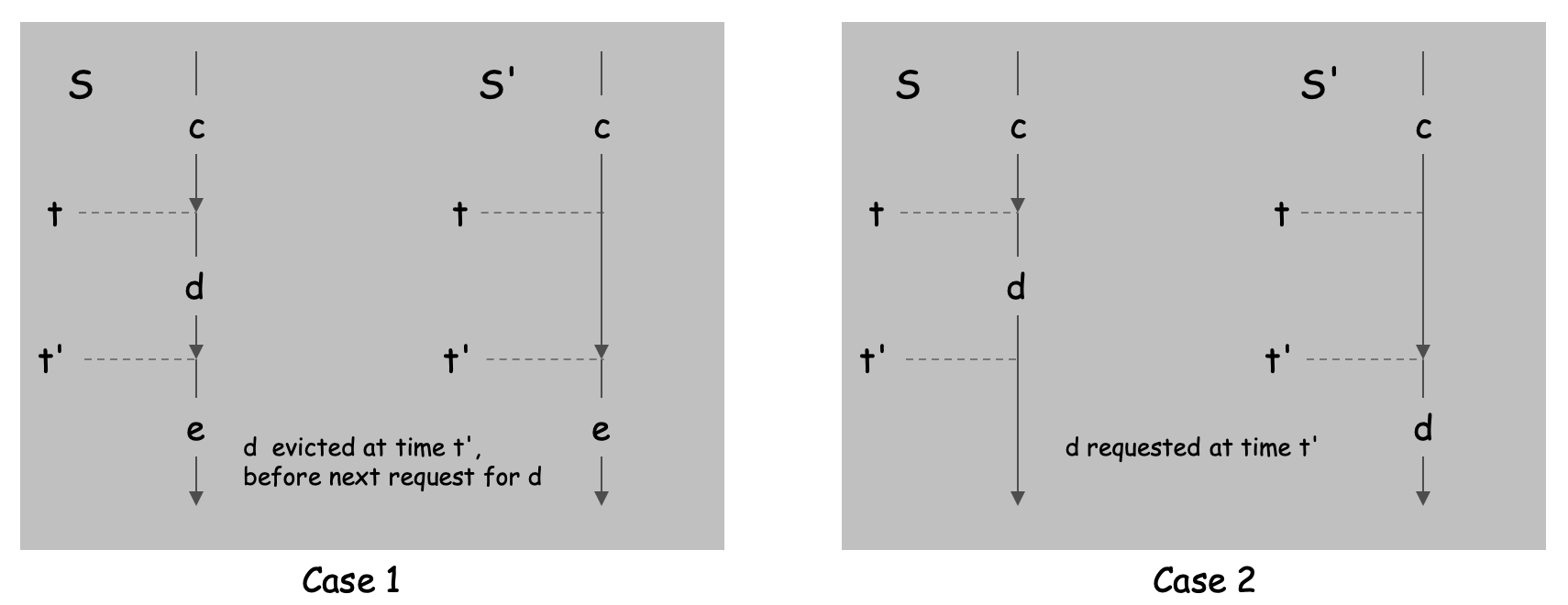
综上，$S$ 可以转化成某简化调度 $S’$，且 miss 总数不增加。

FF 算法的最优性

由上述讨论知，存在最优调度策略，其同时也是简化调度。假设某最优调度策略不是简化策略，可以将该策略转化为简化调度，且 miss 数不增加，则转化后的策略也是最优调度策略（称其为最优简化调度）。

下面证明以下定理（暂且称其为 FF 最优性定理）：

Farthest-in-Future 算法得出的策略 $S_\text{FF}$ 是最优策略。

要证明该定理，我们只需证明（暂且称为 FF 前缀最优定理）：

对任意非负整数 $n$，存在某最优简化调度 $S^*$，使得其前 $n$ 个请求的调度策略和 $S_\text{FF}$ 相同。

用数学归纳法进行证明：

• $n=0$ 时，该命题显然成立。

• $n = j(j \geq 0)$ 时，假设该命题成立，即存在某最优简化调度 $S^*_j$ 满足前 $j$ 个请求的调度策略与 $S_\text{FF}$ 相同，下面尝试构造使命题成立的 $S^*_{j+1}$：

  考虑第 $j+1$ 个请求 $d_{j+1}$，有以下若干种情况：

  1. $d_{j+1}$ 在缓存中，此时 $S^*_{j+1} = S^*_j$ 不做操作，显然和 $S_\text{FF}$ 的前 $j+1$ 个策略相同。

  2. $d_{j+1}$ 不在缓存中，且 $S^*_j$ 和 $S_\text{FF}$ 替换掉相同的 block，则 $S^*_{j+1} = S^*_j$ 和 $S_\text{FF}$ 的前 $j+1$ 个策略显然相同。

  3. $d_{j+1}$ 不在缓存中，$S_\text{FF}$ 替换掉 $e$，$S^*_j$ 替换掉 $f$ 且 $f \neq e$，下面需证明 $S_\text{FF}$ 的策略不比 $S^*_j$ 差：

     构造 $\tilde S^*_{j+1}$ 使得前 $j$ 个请求的调度与 $S^*_j$ 相同、第 $j+1$ 个请求和 $S_\text{FF}$ 相同，假设 $k$ 时刻（$k > j+1$）$\tilde S^*_{j+1}$ 和 $S^*_j$ 第一次执行不同操作，对应请求为 $d_k$。下图为此时两种策略分别对应的缓存状态（$d_{j+1}$ 可能被同时替换成其它 block）：

     

     1. 若 $d_k = e$，容易推出此时 $f$ 没有出现。由于 $S_\text{FF}$ 在第 $j+1$ 个请求时替换了 $e$，则 $e$ 一定比 $f$ 更晚出现，产生矛盾。
     2. 若 $d_k = f$，此时 $f$ 不在 $S^*_j$ 对应的内存中，令 $e’$ 为 $S^*_j$ 替换的 block：
        • 若 $e’ = e$，此时 $\tilde S^*_{j+1}$ 直接从缓存中读取 $f$，二者缓存内容相同。
        • 若 $e’ \neq e$，令 $\tilde S^*_{j+1}$ 将 $e’$ 替换成 $e$，使二者缓存内容相同。此时 $\tilde S^*_{j+1}$ 不是简化调度，但可以由上述讨论在不增加 miss 数的前提下转化成简化调度，并且满足前 $j+1$ 步与 $S_\text{FF}$ 相同**。
     3. 若 $d_k \neq e$ 且 $d_k \neq f$，由于 $\tilde S^*_{j+1}$ 和 $S^*_j$ 执行不同操作，此时 $S^*_j$ 必然替换 $e$。令 $\tilde S^*_{j+1}$ 替换 $f$，则二者缓存内容再次相同。

  综上，可以构造出 $S^*_{j+1} = \tilde S^*_{j+1}$ 使命题在 $n = j+1$ 时成立。

**：人为添加一次替换后，$\tilde S^*_{j+1}$ 在 $k$ 时刻视为出现一次 miss，和 $S^*_j$ 在 $k$ 时刻的请求结果相同；又因为除 $k$ 时刻、$j+1$ 时刻外二者行为一致，显然二者 miss 数相等。此外，为了符号表示方便，转化后的简化调度仍然记作 $\tilde S^*_{j+1}$。

现在 FF 最优性定理的证明变得平凡：只需令 $n = m$，命题显然成立。

后记

在看这个算法的证明时我陷入了两个误区：一是在简化调度部分没有正确理解“不增加 miss 数”的含义：在实际的 CPU 中，换页操作相对于缓存读取是很耗时的，因此现实中的缓存调度采取的也是简化调度的策略以减少不必要的时间开销。二是在所谓“FF 前缀最优定理”的证明中，认为非简化调度 $\tilde S^*_{j+1}$ 的情形下 miss 数被人为增加从而破坏了最优性：实际上由 $\tilde S^*_{j+1}$ 的完整构造过程分析，最优性是得到了保证的。这两个误区我分别添加了星号注解。

这个问题的分析和证明过程恰好反映出贪心算法分析的三大法则：

1. 证明贪心结果不比其它算法差；
2. 最优结果的性质，贪心结果同样满足；
3. 能够在不使答案“变差”的前提下将其它答案转化成贪心答案。

这道题目对于贪心算法的学习还是颇具意义的，虽然记完这个笔记我还是没学会就是了。嗯。