码农的自我修养——插头 DP

想不到促使我学习插头 DP 的动机竟然是一道算法课的 Lab 题，还被网上的假教程演了半天……姑且把学到的东西写一写，纪念一下我对着一屏幕的表画了大半天图的自闭时光。

起这个标题的原因实在一篇博客里看到“转移过程十分码农”，敲完代码深以为然，就借用过来了。

以下内容仅为插头 DP 的一种应用情形。若要应用于其他题目，需要对过程略作修改。

前置知识：状态压缩 DP、BFS、哈希

问题背景

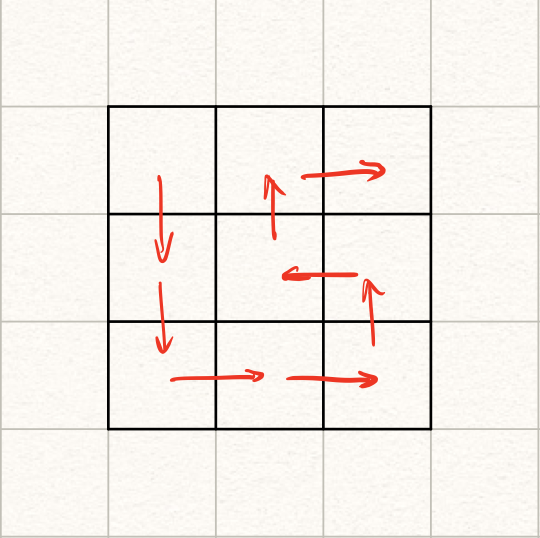
给定一张 $n \times n$ 的有障碍物方格纸（$n \leq 8$），问从 $(1, 1)$ 到 $(1, n)$ 一共有多少条 Hamilton 路径？（为方便后文叙述，此处做了转置处理）

前置概念

插头和括号匹配

把上面的图一切两半，在断口处会有“被切断的路”，这就是这个问题模型里的插头。

为什么会和括号匹配有关系呢？在这张方格纸上画回路（或者 Hamilton 路，额外加一条边就能构成回路）本质上是在构建一张平面图。从断口的一侧看，如果同一条路径与断口的两个交界处看成一组括号，那么在断口上可以得到一组合法的括号匹配序列。这个性质可以由反证法得出，此处略去。

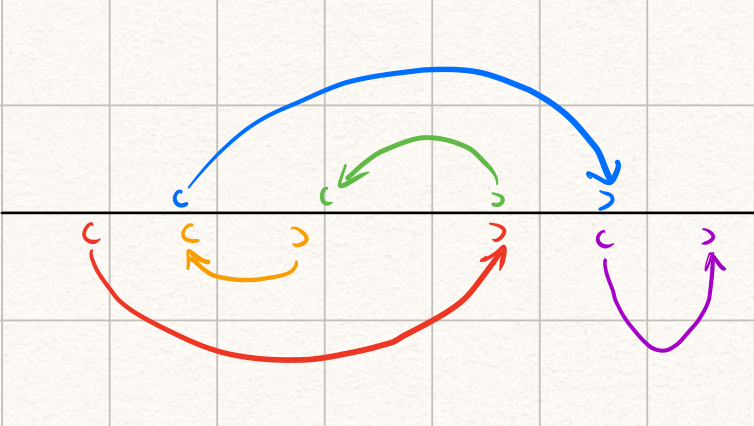
如图，在“断口”的每一侧都能得到一组合法括号匹配序列。因此，我们可以把插头分为两类——“左括号”插头和“右括号”插头。

保证括号匹配合法性是解决题目的关键。

轮廓线

整个搜索过程本质上是一行一行往下扫描的，因此在已遍历部分和未遍历部分中间有一条分界的轮廓线。整个 DP 的过程其实也就是轮廓线的转移过程。假设当前遍历到的格子坐标为 $(i, j)$，那么对应的轮廓线如图：

不难观察到，若方格纸宽度为 $n$，则轮廓线的长度为 $n+1$。特殊地，当 $j = 0$ 时，轮廓线形状如图：

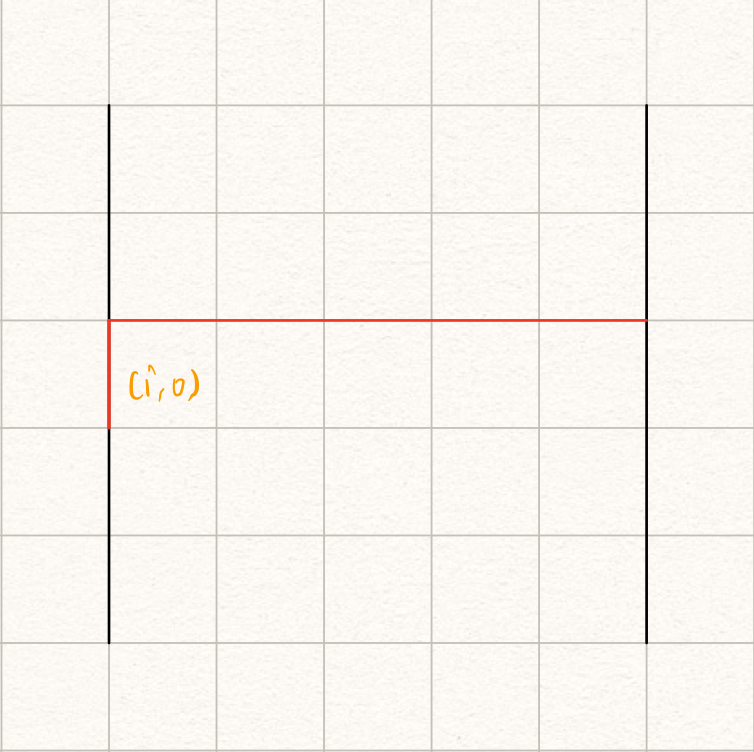
这个特点在后面状态转移的时候会提及。

状态转移

为方便后续描述，记 $0, 1, 2$ 分别为无插头、“左括号”插头（简称左插头）、“右括号”插头（简称右插头）；$\neq 0$ 泛指有插头。

如果轮廓线上的插头状态能用数字 $S$ 来表示，那么我们就可以用 $(i, j, S)$ 来刻画格子 $(i, j)$ 对应的状态了。对于每一个“单元轮廓线”，其状态有三种：没有插头（$0$）、有左插头（$1$）和有右插头（$2$）。为了方便起见，我们可以使用四进制表示，用位运算的方法加快转移。

对于位置 $(i, j)$ 上的方格，其状态转移过程如图（以 $n = 5$ 为例）：

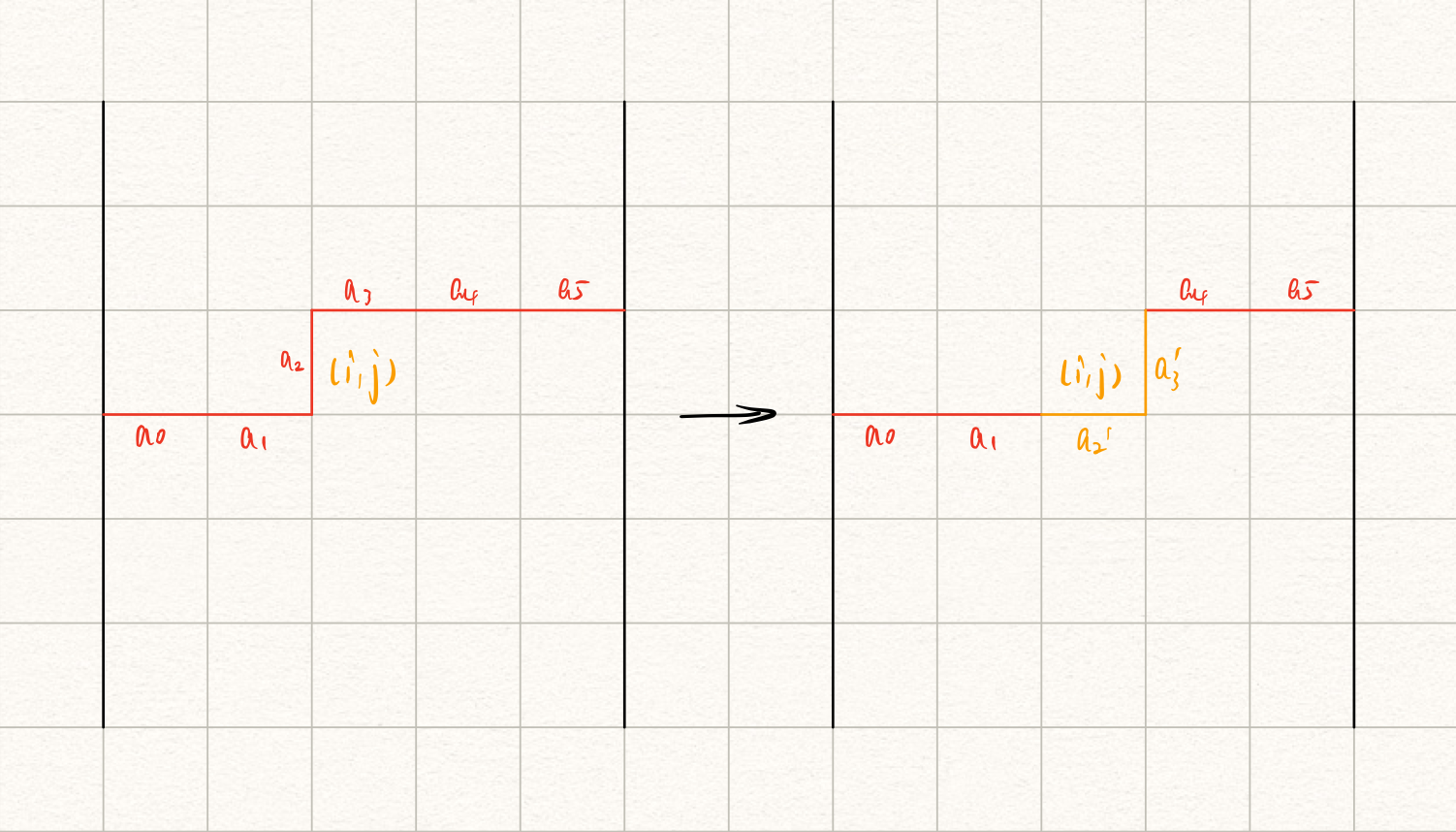
特殊地，当 $j = n$ 时，我们发现有一条轮廓线竖直贴到了最右边。这并不是我们期望的状态，所以需要做一下修正：

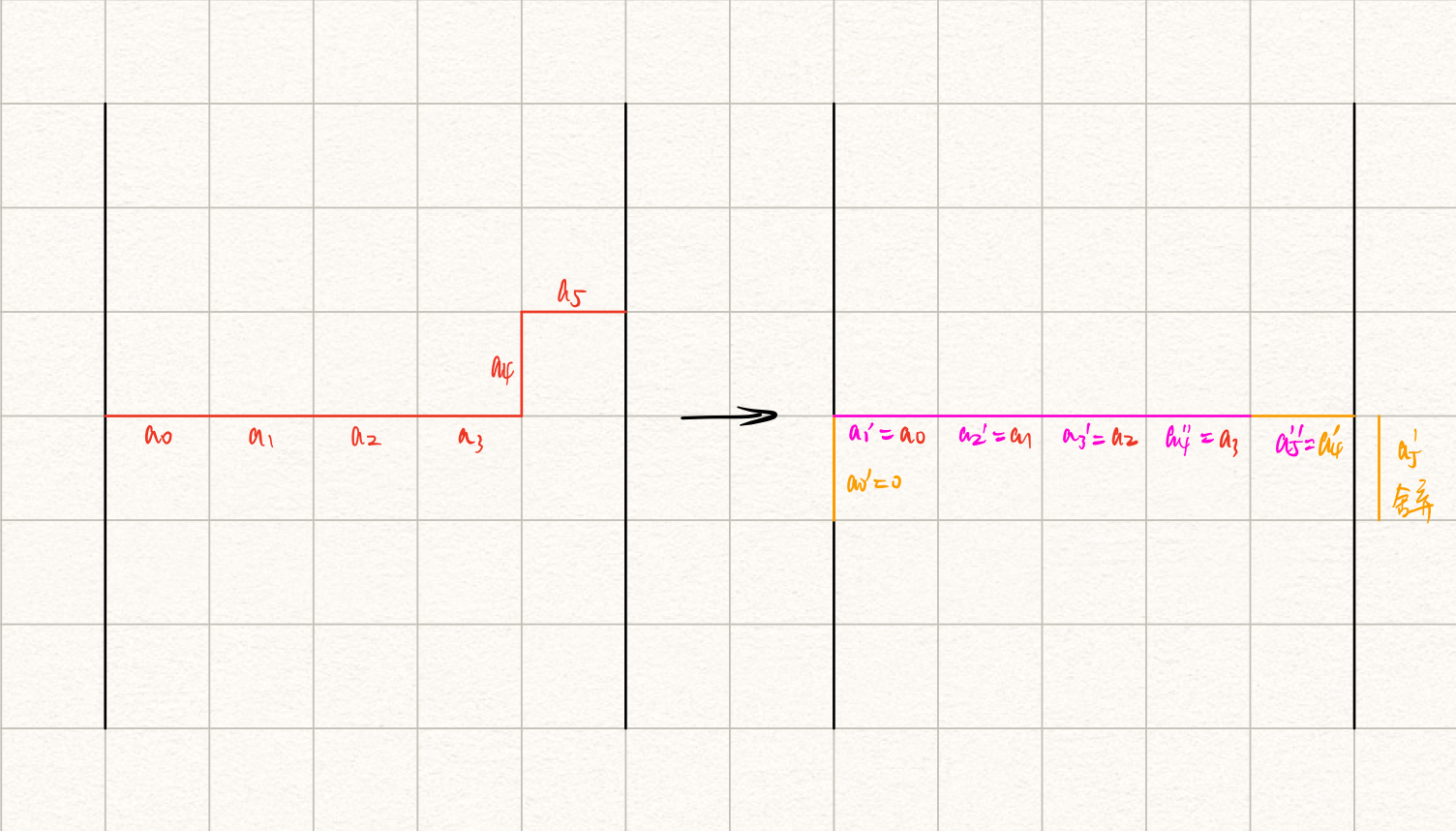
注意对应下标的变化，对应到 $S$ 上需要做移位操作（四进制）。整个过程其实就是一行一行扫描的过程。

由于上一行的 $a'_n$ 会被舍去，所以 $a'_n \neq 0$ 的状态是非法的。转移的时候要注意。

如果沿用上面的标记，那么初始状态就应该是 $a_1 = 1, a_n = 2$，其余地方均为 $0$。我们给这个状态初始化为 $1$，表示这样的状态有一种可能性。该状态如图所示：

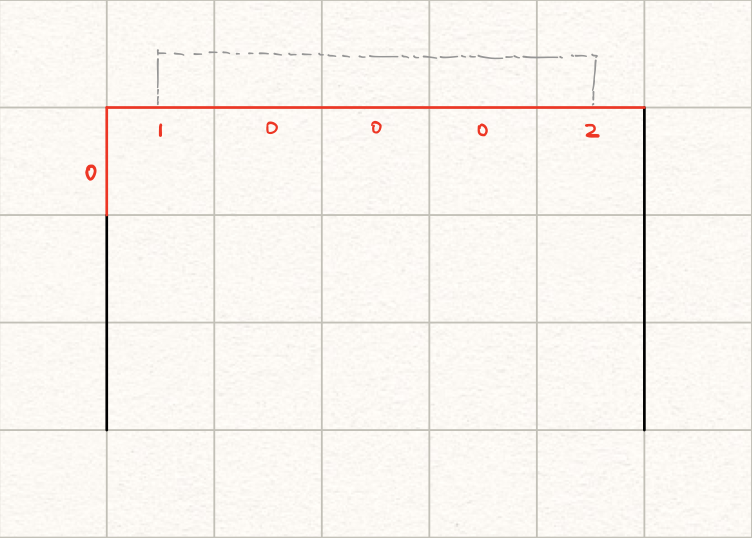
在上方人为添加一条线，实际上就成了 Hamilton 回路问题。

---

接下来的部分，就是非常码农的状态转移了。

啰嗦一句，这里的状态转移就是把当前状态 $S$ 的情况数累加到下一个状态 $S'$ 上，前提是通过对当前格子的操作可以使 $S$ 变成 $S’$。

由于每次转移只有两个插头发生了变化（忽略换行的情形），我们可以把这些情形全部枚举出来一一讨论（红色代表 $S$，橙色代表 $S’$）：

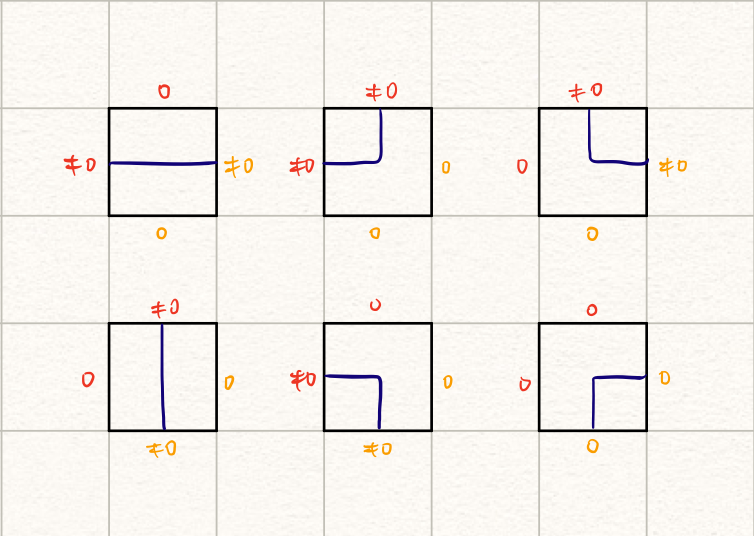
1. $(\neq 0, 0)$ 的情形

   只有一个插头的情形，只需要把这个插头（对应的路）拓展一格就好了。我们可以向下做拓展：

   

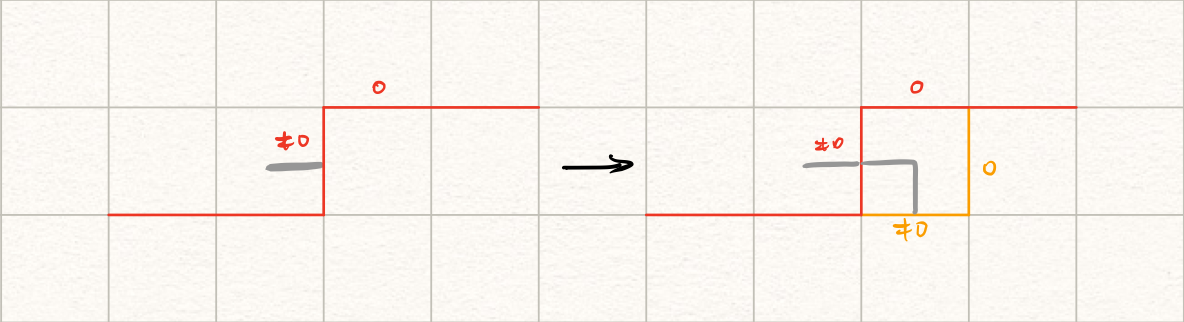
   注意拓展后的插头类型和拓展前一致。如果当前 $j \neq n$，还可以向右做拓展：

   

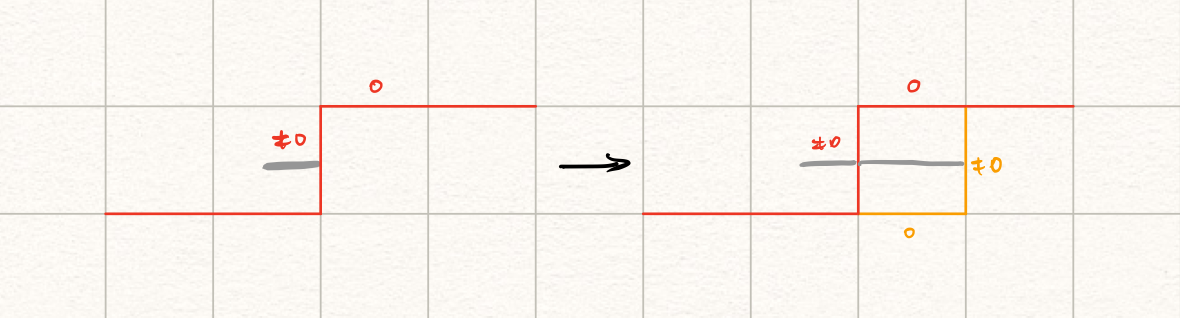
   写成数学符号的形式就是：

   $$(\neq 0, 0) \rightarrow \begin{cases} (\neq 0, 0)\\ (0, \neq 0) \text{ if } j \neq n \end{cases}$$

2. $(0, \neq 0)$ 的情形

   和上面的情形一样，可以向下或者向右（若 $j \neq n$）拓展：

   

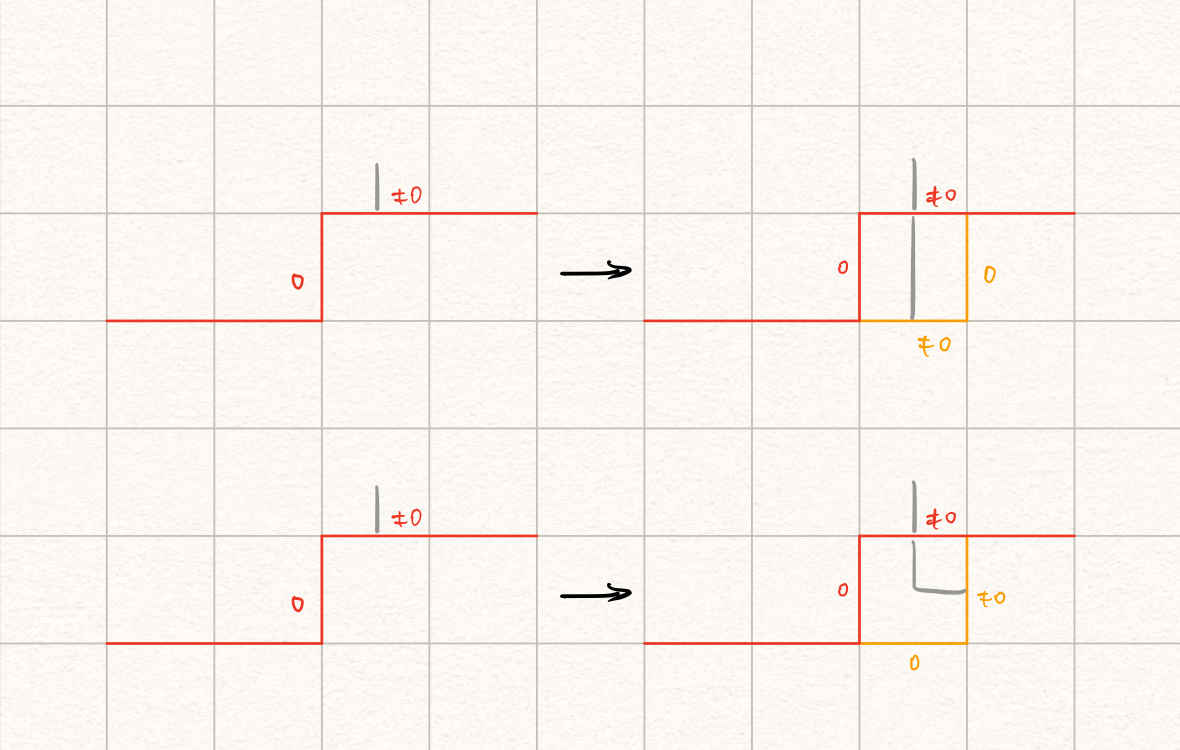
   用符号表达就是：

   $$(0, \neq 0) \rightarrow \begin{cases} (\neq 0, 0)\\ (0, \neq 0) \text{ if } j \neq n \end{cases}$$

3. $(0, 0)$ 的情形

   如果两边都没有插头，那就只能 自力更生 新建插头了。为了适应后面的转移，定义新插头状态为 $(1, 2)$：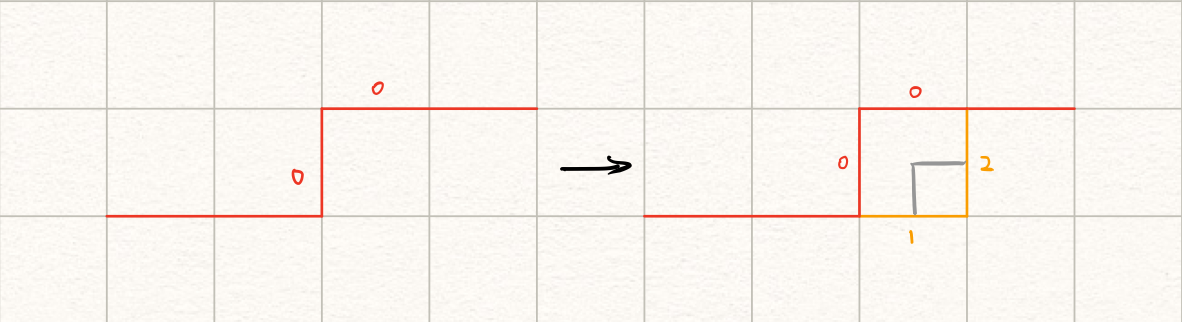

   

   符号表达：

   $$(0, 0) \rightarrow (1, 2) \text{ if } j \neq n$$

4. $(\neq 0, \neq 0)$ 的情形

   两个插头的情形，只要把这两个插头接起来就大功告成了？

   

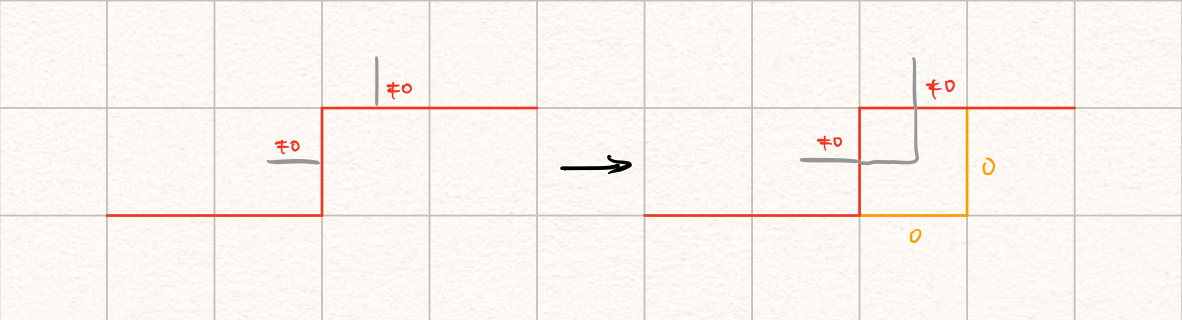
   符号表达：

   $$(\neq 0, \neq 0) \rightarrow (0, 0)$$

   错！

   对于当前题目，我们需要的是一条 Hamilton 路，也就是说中间不能出现其它回路。因此我们需要格外注意括号配对的问题。

   下面对四种情况进行分类讨论：

   • $(2, 1)$ 的情形

     右插头和左插头连接（注意顺序），其实是把两段独立的线接在了一起。没有问题，直接转移。

   • $(1, 1)$ 的情形

     左插头和左插头连接，意味着从起点出发的线和一条独立的线接在了一起，作为一条新的起点出发的线。于是我们需要对这条线进行一下修正：

     

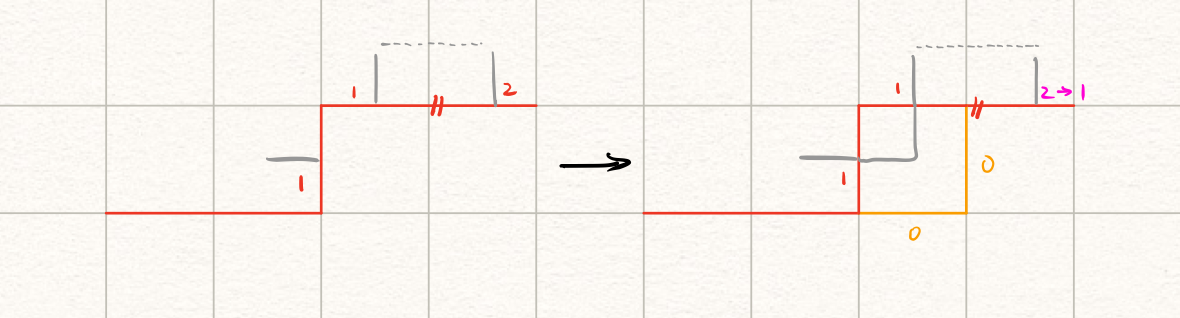
     如图所示，右边的这个 $1$ 有一个对应的 $2$，我们需要将其修改为 $1$。我们可以由括号匹配法则向右搜索找到这个 $2$。这样一来，整个轮廓线上的括号匹配合法性也得到了保证。

   • $(2, 2)$ 的情形

     同理，我们需要对左边的 $2$ 对应的线进行修正。由括号匹配法则向左找到匹配的 $1$ 并修改成 $2$。

     

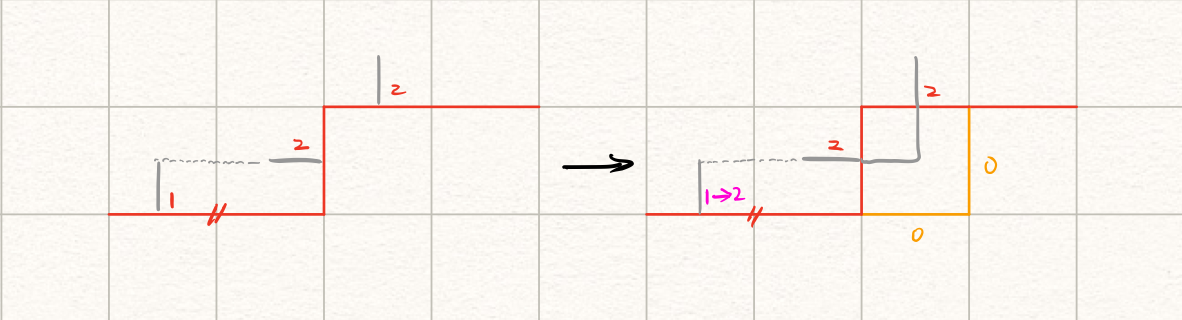
   • $(1, 2)$ 的情形

     左插头和右插头连接，意味着一个回路的闭合。在这道题目里，我们只能在最后一个遍历到的方格完成这个操作，其余的情况都不能做转移，需要剪枝。

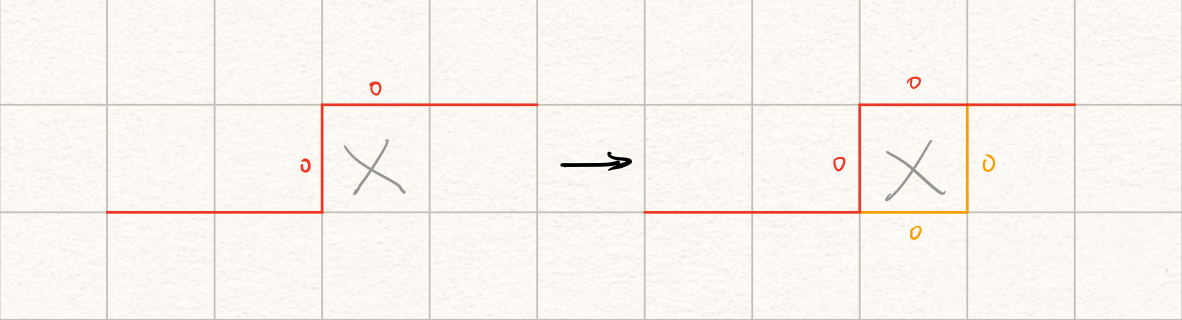
5. 障碍物的情形

   障碍物意味着线路需要绕过当前方格，因此也需要状态转移。唯一合法的转移只有 $(0, 0) \rightarrow (0, 0)$。

   

最终只需要检查 $(n + 1, 1, 0)$ 这个状态的值就完成了。（应该也可以检查 $(n, n, ?)$ 的状态吧？依实现情况而定）

空间优化

DP 一般的做法是使用数组（dp[i][j][S]）来进行转移；然而在这道题里，暴力开数组是会 MLE 的！

然而经过观察，在整个状态空间里面实际用到的状态数并不多，因此我们可以考虑使用哈希表和队列来维护需要转移的状态（有 BFS 那味了）。鉴于这里不是 ACM，调标准库的unordered_map/HashMap和queue/Queue不香吗？

由题意，$n \leq 8$，因此刻画 $S$ 最多需要 18 个二进制位，而 $i$ 和 $j$ 最多分别需要 4 个二进制位。int范围刚好存的下，这样就可以把这个三元组转换成整数来做哈希了。

需要注意的一点是，状态转移过程中有可能出现多个状态指向一个状态的情形，也就是说一个状态有可能多次入队、进行重复转移！这就需要考虑到 DP 的核心——记忆化搜索了。同样地，由于无法开数组来标记入队信息，可以使用unordered_set/HashSet来记录已入队的状态，从而规避重复入队的情况。

接下来只需要像一只码农一样快乐 coding 就好啦！祝各位 dalao 早日 AC！（逃）